论文要点

论文提出了一个统一框架来刻画 self-play（智能体与自身或自身历史版本交互以改进策略）的各种方法，按策略更新机制、对手选择与人口管理、博弈类型（零和/非零和、可转性/非可转性）等维度进行分类，并回顾了代表性算法、应用场景与理论/实践挑战，同时列出了未来研究方向与评估指标。

形式化背景（模型与博弈概念）

多智能体/博弈框架：论文以一般性多智能体强化学习（MARL）和博弈论为基础，区分正规型（normal-form）/扩展型（extensive-form）博弈、静态/动态、阶段化/重复博弈等概念，以便统一描述 self-play 在不同博弈结构下的行为与目标（例如寻找纳什均衡、演化稳定策略或弱优势策略）。

可转性（transitive） vs 非可转性（non-transitive）：可转性指“若A优于B、B优于C则A优于C”的链式优先关系；许多对抗任务（尤其多人博弈、策略游戏）表现非可转性，因此简单的梯度上升/自我复制容易陷入循环/无提高。论文把这一点作为自我对战设计（population /league）与评估设计的重要动因。

统一框架与分类

论文提出一个把 self-play 方法放入统一座标系的框架，主要维度包括：

对手/人口（Opponent/Population）策略的来源

单一历史版本（vanilla self-play）

历史平均策略 / 轨迹记忆（fictitious-play / NFSP）

人口/联盟（population/league）机制（AlphaStar、OpenAI Five 等）

元策略/元博弈（PSRO 等基于 meta-game 的方法）

策略更新 / 学习模式（Policy Update）

直接基于 RL（PPO/PG/Q-learning）自对弈更新

模仿/监督学习成分（例如把历史胜利轨迹当作专家样本）

混合：监督 + 强化（如 NFSP 的 supervised policy + RL best-response）

解算目标（Solution Concept）

逼近纳什均衡（Nash）/最小最大解

训练一个强策略以击败特定对手集合（best-response / exploiters）

环境 /博弈类型（棋类、卡牌、MOBA、视频游戏等）——不同任务偏好不同 self-play 策略。

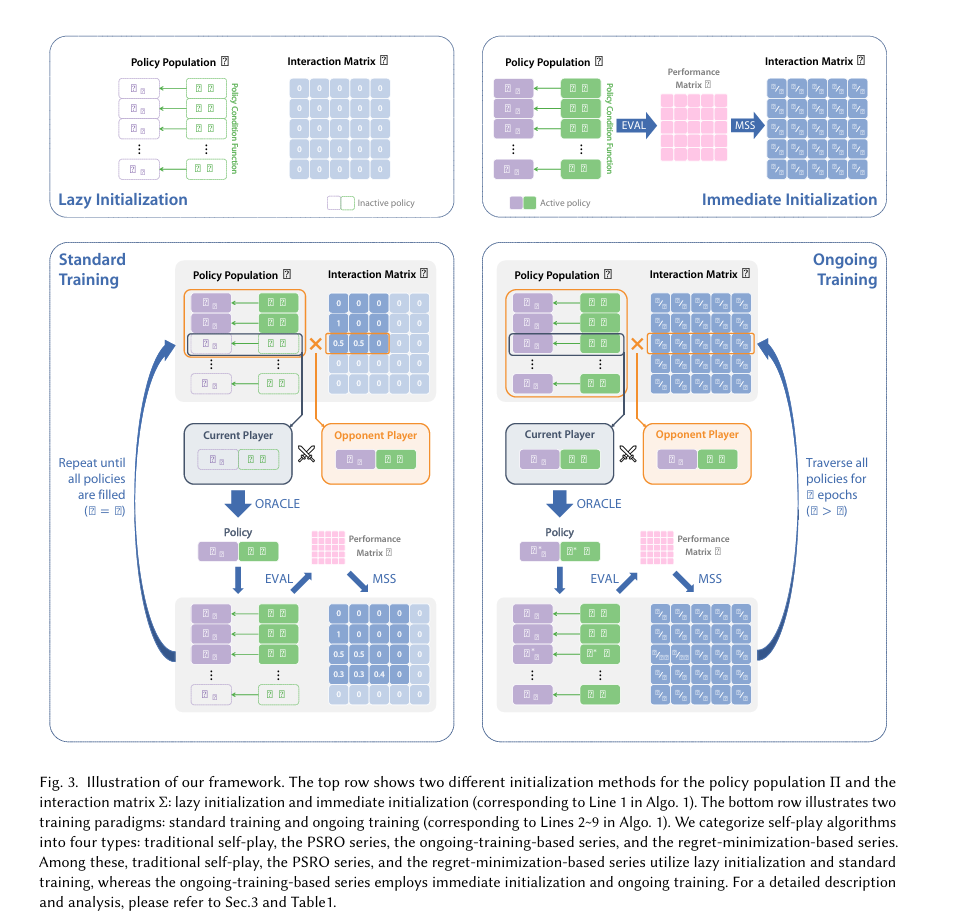
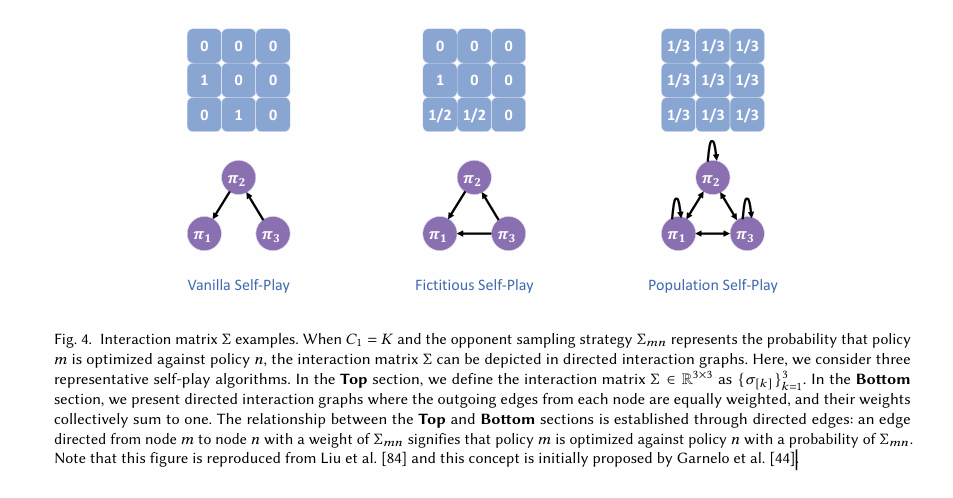
论文在该框架下把大量算法（vanilla SP、fictitious SP、NFSP、PSRO、CFR 及其变体、league/population methods、time/space saving CFR、MCCFR、NeuPL、FTW 等）放入对应类别，并分析各自优缺点与适用场景。

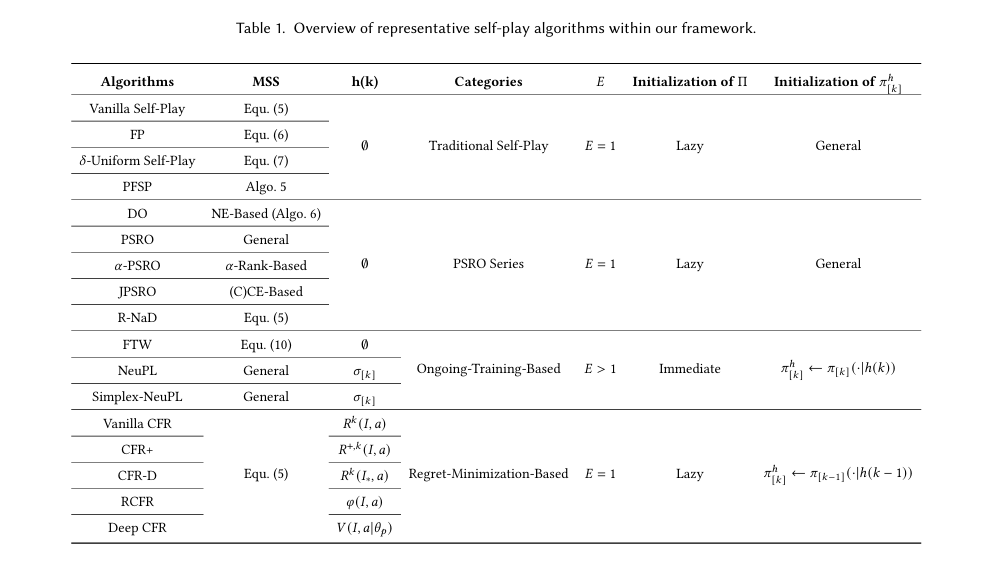
主要 self-play 方法与技术要点

下面列出论文重点讨论的几大类方法，并给出实现/算法层面的要点与工程注意事项。

1) Vanilla Self-Play（原始自我对战）

核心思想：当前策略与其自身副本或最新版本对战，直接用 RL（如 PPO、A2C）在自对弈数据上更新策略（常见于 AlphaZero 的早期流程）。

优点：实现简单，能自动构造 curriculum（对手随进化自动变难）。

缺点：在非可转性/多样对抗环境中会收敛到循环、被 exploit 或出现退化（在复杂多人博弈中尤甚）。

工程要点：需要维护版本管理（checkpoint、对战匹配规则），以及稳定化手段（学习率、熵正则、对手采样机制）。

2) Fictitious Play / Neural Fictitious Self-Play (NFSP)

核心思想：经典“虚构博弈（fictitious play）”思想：以对手策略的历史平均作为对手分布来训练 best-response。NFSP 用神经网络表示策略与平均策略（用监督学习逼近历史策略分布），将 RL 的 best-response 与监督学习分离训练。

优点：理论上更接近收敛到纳什（在某些零和/对称设置），缓和了非可转性问题。

实现细节：需要双网络（RL network + supervised average network）、经验缓冲区的设计（保存轨迹以学习平均策略）、与RL更新时序的协调。

3) PSRO（Policy-Space Response Oracles）及其变体

核心思想：把博弈抽象成meta-game（策略集合的收益矩阵），迭代地：计算 meta-game（通过自我对战/仿真估计收益），对 meta-game 求解（找到混合策略），然后训练一个 oracle（最优响应网络）对抗当前混合策略，加入人口，重复。PSRO 是对 Double-Oracle、Fictitious Play 的现代扩展。

技术点：

估计 payoffs 的样本效率和方差控制（需要大量自对弈）

meta-solver 的选择（怎样从 payoff matrix 提取混合策略；Nash solver / regularized solver）

oracle 的训练方式（RL、imitation）、以及人口管理（何时淘汰/保存策略）

适用性：擅长处理非可转性问题并能显式控制策略多样性，适用于复杂对抗任务。

4) Counterfactual Regret Minimization (CFR) 及变体（扑克类成功范式）

核心思想：用于不完全信息博弈（如扑克），通过在线/离线估计每个信息集下的 regrets，反复最小化后收敛到近似纳什。MCCFR/抽样变体用于规模化；还有 time-saving / space-saving 版本优化效率。

工程实践：扑克类大型系统（Pluribus、Libratus）用了 CFR 或 MCCFR 的工程化版本 + 大规模并行 /资源调度与抽样策略。论文对这些变体和工程技巧做了整理。

5) Population / League Methods（人口/联盟训练）

例子：AlphaStar（league training）、OpenAI Five（league + exploiters）、MuZero/AlphaZero 的变体。

关键思想：维护一个策略人口（包括主策略、历史均值、专门的 exploiters、随机对手等），通过对不同对手的有针对性训练提高鲁棒性并避免过拟合单一对手。

工程要点：策略选择/采样分布、人口增长/修剪策略、如何生成挑战性对手（exploiters）、以及如何保证训练稳定（避免 population collapse）。

6) 混合方法与近期创新（NeuPL、FTW、R-NaD 等）

近期工作尝试模块化、用元学习或基于神经方法学习 population 管理策略、自动化对手生成/筛选策略（论文列出了若干具体方法与评测）。这些方法往往在复杂视频游戏/多人 MOBA 中表现更好。

代表性系统与实现要点

论文里有一张表格列出众多代表性系统（AlphaGo/AlphaZero/MuZero、OpenAI Five、AlphaStar、Pluribus、DeepStack、Libratus、TiZero、DeltaDou 等），并以游戏类别、参与方信息、是否使用专家数据、使用的 self-play 类别等维度比较。关键实现经验（从这些系统总结）包括：大量并行自对弈仿真、版本管理与checkpointing、专门的 exploiters/league 设计、meta-game 解析（PSRO）等。

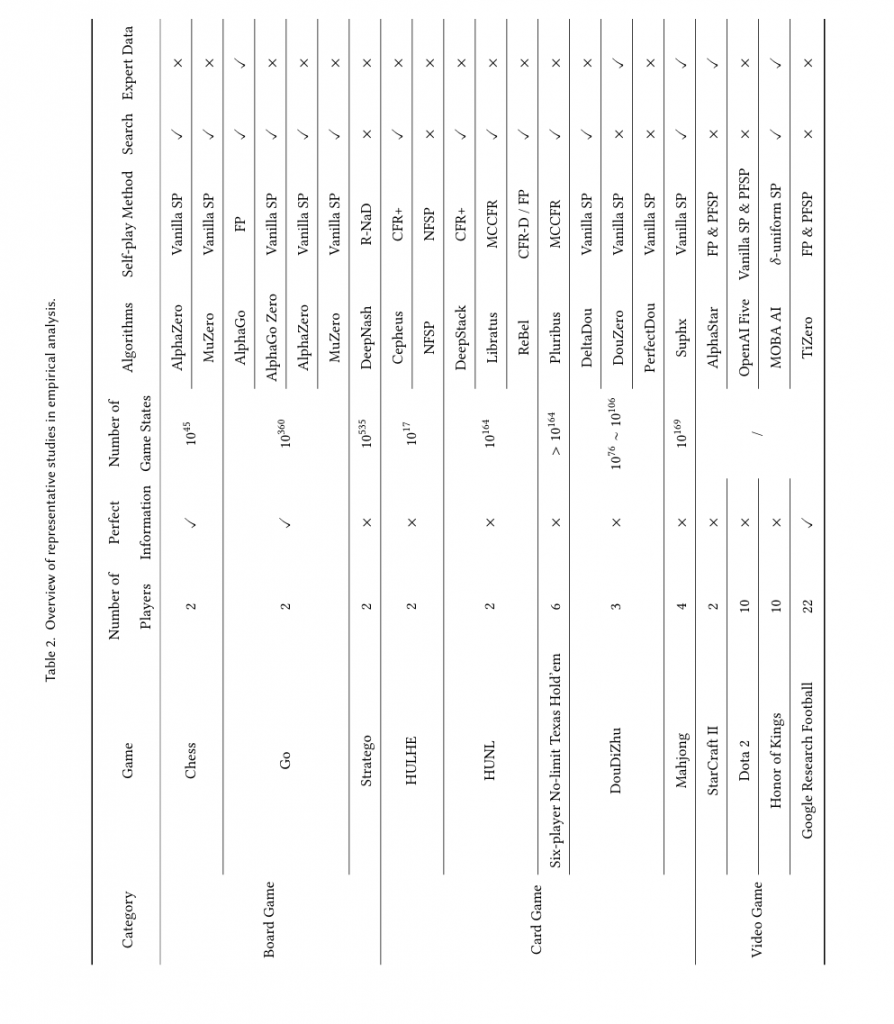
评估指标与实验设计

论文讨论了评估 self-play 策略的若干指标与实践方法，包括：

NashConv：衡量距离纳什均衡的差距（尤其在零和博弈中常用）。

Exploitability / exploit rate：衡量能否被 exploiter 打败（越低越鲁棒）。

Head-to-head win rate / ELO / Glicko：直接对弈强度度量（但对非转性游戏可能误导）。

Population-level coverage / diversity metrics：衡量策略人口覆盖策略空间的程度（有助于判断是否解决非转性循环）。

样本效率 /计算消耗 /并行化开销：在工程实践中非常关键。

主要挑战（论文总结的研究空白）

论文列出并讨论了若干未解决或未充分解决的问题：

非可转性与循环动态：如何构建能在高度非转性环境中稳健增长的训练流程？（PSRO/Population 提供方向，但样本/计算代价高）

样本/计算效率：大规模自对弈非常昂贵，如何用更样本高效的 meta-solvers、估计器或模拟器减少成本？

收敛性与理论保证：许多方法在实践有效但缺乏广泛的理论收敛保证（尤其在非零和、多玩家场景）。

评估基准不完善：缺乏覆盖现代 self-play 方法所有能力的综合 benchmark，尤其针对多人、非零和与非可转性的场景。

从模拟到现实（Sim2Real）与在人类—机器交互的鲁棒性：真实世界应用（机器人、经济学模拟）仍面临转移问题。

结论与论文贡献

这篇 survey 系统化了 self-play 的研究景观，从形式化定义到统一框架、从算法分类到代表性系统与评估实践、从工程经验到理论与现实挑战，给出了一张清晰的“地图”供研究者与工程团队选择方法、设计实验与识别研究空白。论文同时指出 PSRO / population-based methods 在应对非可转性方面的潜力，以及在样本/计算效率与理论保障方面亟需改进的问题。